球体メッシュを生成できるようにします。
プログラムはこちらで公開しています。
https://github.com/matsushima-terunao/opengl_sample
球体メッシュ作成
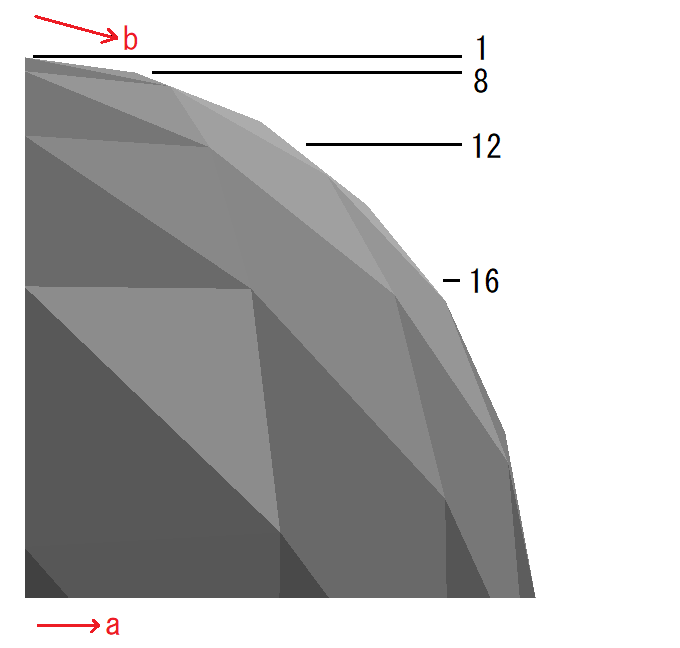
球体を緯度方向と経度方向に分割してポリゴンを作成します。
/**
* 球体メッシュ作成。
*/
void create_sphere_mesh(
int width, int height, int vert_height, int texture_width_bits, int surfaces, const int* texture, const int* palette,
int div_a0, int div_da, int div_b,
float*& verts, size_t& verts_count, size_t& verts_stride, int*& polys, size_t& polys_count
) {
std::cout << "< create_sphere_mesh:unit=" << texture_width_bits << ",width=" << width << ",height=" << height << std::endl;
clock_t time1 = clock();
int texture_width = 1 << texture_width_bits;
int stride = 11;
//16, 4, 8 * 8
//verts=36357,p=36357
//polys=71633,p=71633
int p, d, a, b, div_a;
// 頂点バッファを初期化する
p = surfaces * stride;
div_a = div_a0;
for (b = 1; b <= div_b; ++b, div_a += div_da) {
p += surfaces * stride * div_a; // d = -1,1: color, x, y, z
}
verts = new float[p];
verts_count = p * sizeof(float) / 11;
p = 0;
for (d = -1; d < surfaces; d += 2) {
for (b = 0; b <= div_b; ++b) {
double y = height / 2.0 * cos(M_PI / 2.0 * b / div_b) * d;
double r = width / 2.0 * sin(M_PI / 2.0 * b / div_b);
div_a = (0 == b) ? 1 : div_a0 + (b - 1) * div_da;
std::cout << div_a << std::endl;
for (a = 0; a < div_a; ++a) {
double x = r * cos(2.0 * M_PI * a / div_a);
double z = r * sin(2.0 * M_PI * a / div_a);
int texture_u, texture_v;
int c = get_color_by_celestial_coordinate(
texture_width, 2.0 * M_PI * a / div_a, (float)b / div_b, surfaces,
texture, texture_u, texture_v);
double h = 1.0;
if (palette) {
h = 1.0 + (double)c * vert_height / 256.0;
c = palette[c];
}
verts[p++] = (float)(x * h);
verts[p++] = (float)(y * h);
verts[p++] = (float)(z * h);
verts[p++] = ((c >> 16) & 255) / 255.0f;
verts[p++] = ((c >> 8) & 255) / 255.0f;
verts[p++] = ((c >> 0) & 255) / 255.0f;
verts[p++] = (float)texture_u / texture_width;
verts[p++] = (float)texture_v / texture_width;
double len = sqrt(x * x + y * y + z * z);
verts[p++] = (float)(x / len);
verts[p++] = (float)(y / len);
verts[p++] = (float)(z / len);
}
}
}
std::cout << "verts_count=" << verts_count << ",p=" << p << ",div_a=" << div_a << std::endl;
// インデックスバッファを初期化する
p = surfaces * 3 * div_a; // p0, p1, p2[, p0, p2, p1] ...
div_a = div_a0;
for (b = 1; b < div_b; ++b, div_a += div_da) {
p += surfaces * 3 * 2 * div_a; // d = 0,1
}
polys = new int[p];
polys_count = p;
p = 0;
int p0, p1 = 0;
for (d = 0; d < surfaces; ++d) {
p0 = p1;
p1 = p0 + 1;
div_a = div_a0;
for (a = 0; a < div_a; ++a) {
polys[p + 0] = p0;
assert(p + 1 + d < polys_count);
polys[p + 1 + d] = p1 + a;
polys[p + 2 - d] = p1 + (a + 1) % div_a;
p += 3;
}
p0 = p1;
p1 = p0 + div_a;
for (b = 1; b < div_b; ++b, div_a += div_da) {
for (a = 0; a < div_a; ++a, ++p0, ++p1) {
polys[p + 0 + d] = p0;
polys[p + 1 - d] = p1;
polys[p + 2] = p1 + 1;
p += 3;
polys[p + 0] = p0;
polys[p + 1 + d] = p1 + 1;
polys[p + 2 - d] = (div_a - 1 != a) ? p0 + 1 : p0 + 1 - div_a;
p += 3;
if (0 == (a + 1) % (div_a / div_da)) {
polys[p + 0] = (div_a - 1 != a) ? p0 + 1 : p0 + 1 - div_a;
polys[p + 1 + d] = p1 + 1;
polys[p + 2 - d] = (div_a - 1 != a) ? p1 + 2 : p0 + 1;
p += 3;
++p1;
}
}
}
}
verts_stride = stride * sizeof(float);
std::cout << "polys_count=" << polys_count << ",p=" << p << ",div_a=" << div_a << std::endl;
std::cout << "> create_sphere_mesh(): time1=" << ((double)time1 / CLOCKS_PER_SEC) << std::endl;
#if 0
// 結果dump
float div = 500.0f;
std::cout << std::fixed;
for (int i = 0; i < verts_count / 4; ++i) {
std::cout << "v " << verts[i * 11] / div << " " << verts[i * 11 + 1] / div << " " << verts[i * 11 + 2] / div << std::endl;
}
for (int i = 0; i < verts_count / 4; ++i) {
std::cout << "vt " << verts[i * 11 + 6] << " " << verts[i * 11 + 7] << std::endl;
}
for (int i = 0; i < verts_count / 4; ++i) {
std::cout << "vn " << verts[i * 11 + 8] << " " << verts[i * 11 + 9] << " " << verts[i * 11 + 10] << std::endl;
}
for (int i = 0; i < polys_count / 3; ++i) {
std::cout << "f " << polys[i * 3 + 0] + 1 << "/" << polys[i * 3 + 0] + 1 << "/" << polys[i * 3 + 0] + 1;
std::cout << " " << polys[i * 3 + 1] + 1 << "/" << polys[i * 3 + 1] + 1 << "/" << polys[i * 3 + 1] + 1;
std::cout << " " << polys[i * 3 + 2] + 1 << "/" << polys[i * 3 + 2] + 1 << "/" << polys[i * 3 + 2] + 1 << std::endl;
}
exit(0);
#endif
}
極座標からテクスチャーの色・UV座標を取得
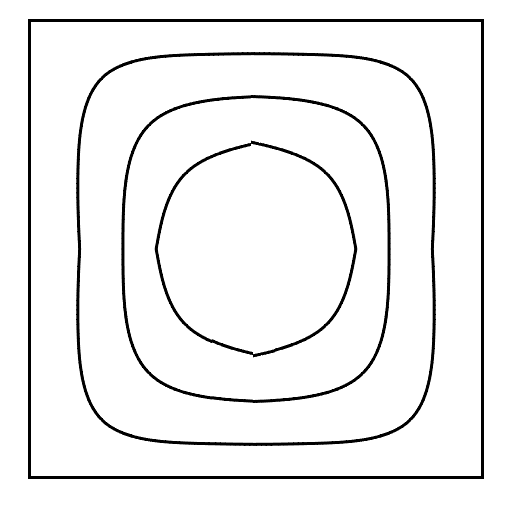
北極・南極地点を中心とし、赤道を四辺として座標変換を行い、頂点の色とUV座標を求めます。
/**
* 極座標からテクスチャーの色・UV座標を取得。
*
* @param texture_width テクスチャーの解像度
* @param a 偏角(経度)
* @param r 動径(緯度)
* @param surfaces 1:北半球のみ 2:北半球+南半球
* @param texture_buffer テクスチャーのピクセルデータ
* @param color_palette テクスチャーのカラーパレット
* @param ptx テクスチャーのU座標へのマッピング配列
* @param pty テクスチャーのV座標へのマッピング配列
* @param p ptx, pty への格納インデックス
* @return テクスチャーの ARGB
*/
static int get_color_by_celestial_coordinate(
int texture_width, double a, double r, int surfaces,
const int* texture_buffer, int& texture_u, int& texture_v) {
double ra = 1.0;
if (2 == surfaces) {
// 円から矩形へ伸張
ra = fmod(a, M_PI / 2);
ra = cos(ra < M_PI / 4 ? ra : M_PI / 2 - ra);
}
// 極座標から直交座標へ変換
int x = (int)((r / ra * cos(a) + 1) * texture_width / 2);
int y = (int)((r / ra * sin(a) + 1) * texture_width / 2);
// 4点の色を平均
int color = 0, i;
for (i = 0; i < 4; ++i) {
x = std::min(texture_width - 1, (2 == i) ? x + 1 : x);
y = std::min(texture_width - 1, (3 == i) ? y + 1 : y);
color += (texture_buffer[x + texture_width * y] >> 2) & 0x003f3f3f;
if (0 == i) {
texture_u = x;
texture_v = y;
}
}
return color;// | (255 << 24);
}
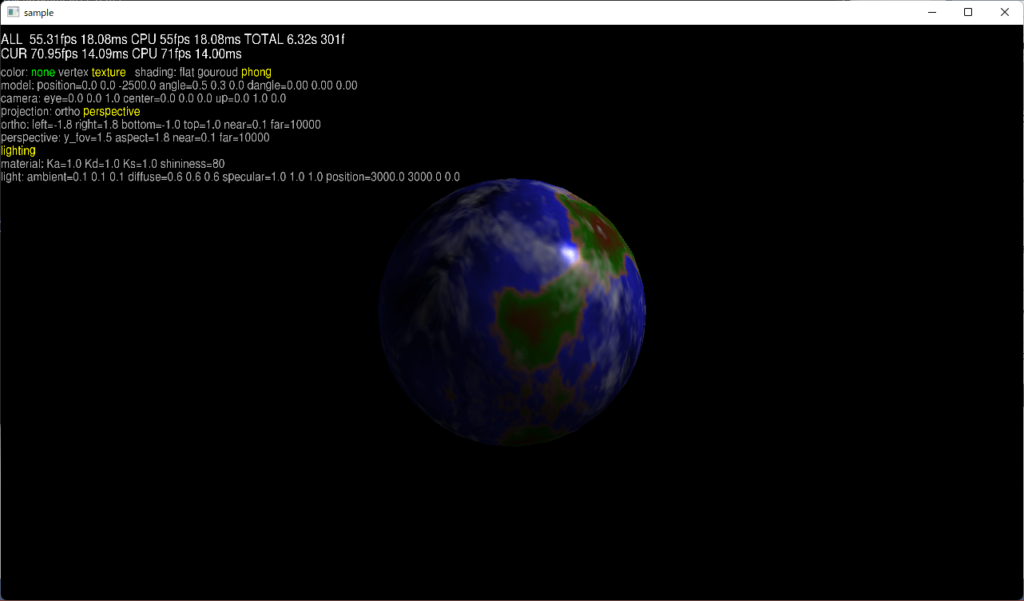
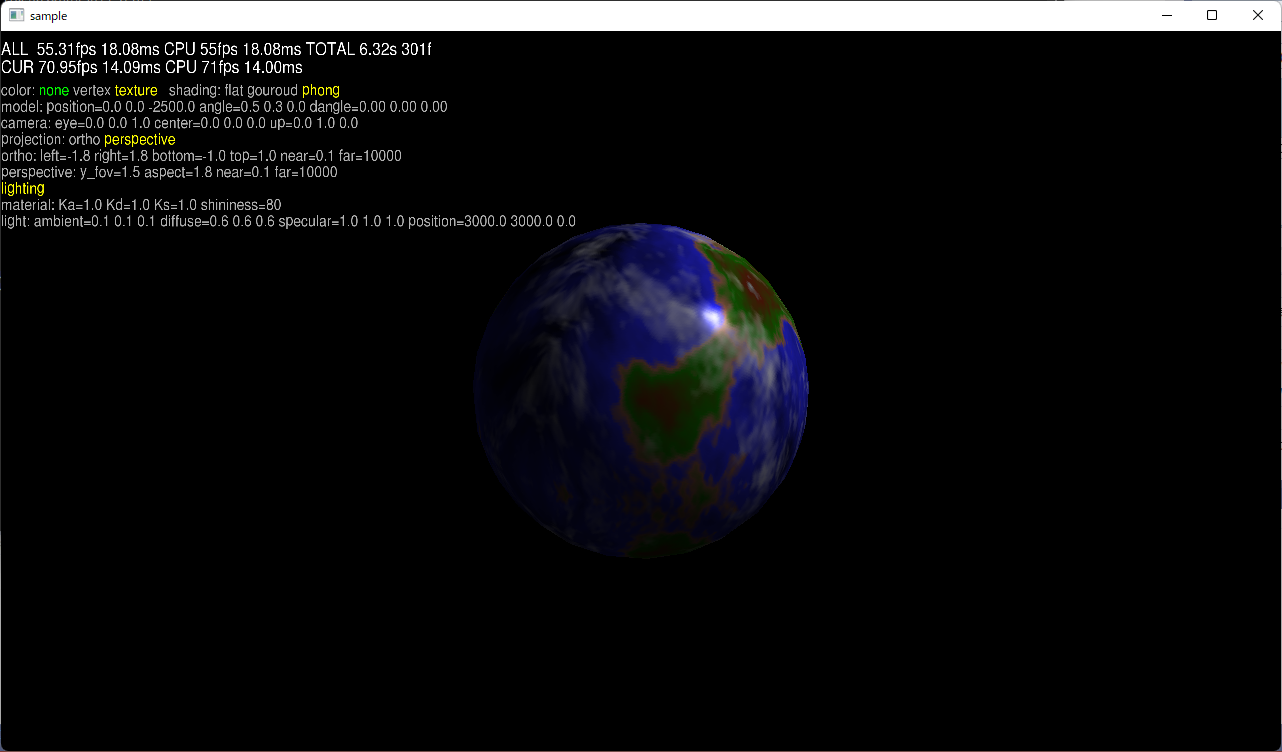
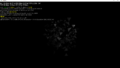
実行結果

コメント